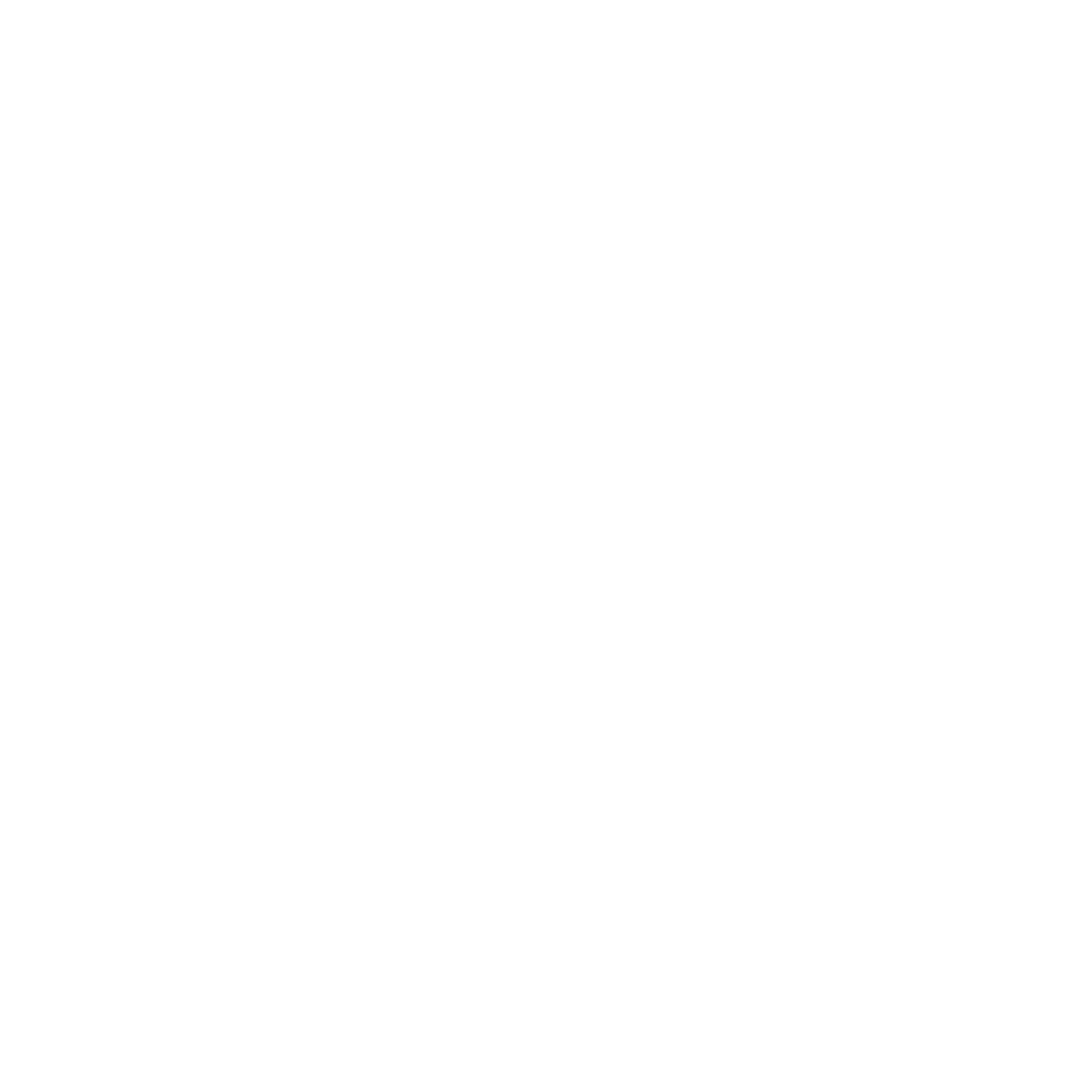The big K-12 education "reform" legislation passed this session was SB 5895, establishing a uniform system of evaluating teacher performance... because who doesn't want to separate the good teachers from the bad, right? I mean with uniform teacher evaluations, principals can work with the underperforming teachers to help them improve—or more likely, fire them, or harass them into quitting. But either way, it's hard to argue against at least knowing how our teachers are doing. Knowledge is power!
Except, how exactly does one objectively measure a teacher's performance when it's the students who are actually taking the tests?
One metric is based on the "value-added model" (VAM), which, according to the Gates Foundation (which absolutely loves VAM) attempts to statistically measure the impact of a teacher on student achievement by adjusting for each student's starting point coming into the class, and then comparing the student's improvement to similar students elsewhere. If a teacher's students outperform their peers, that constitutes positive student growth or "value-added."
Given the Gates Foundation's advocacy, it's not surprising that SB 5895 appears to adopt this approach, mandating that "student growth data must be a substantial factor in evaluating the summative performance of certificated classroom teachers..."
So how reliable are the VAM formulas already in use elsewhere? According to a huge dump of teacher evaluation data recently released by the New York public schools, not so much. Over at TeachForUs.org, a blog serving Teach for America alumni, Gary Rubinstein has been analyzing NYC's value-added data, and finding it surprisingly useless. For example, take the following scatter plot he generated of 665 teachers who taught the same subject at two different grade levels during the same year (2010). The x-axis represents the teacher's VAM score for one class, and the y-axis represents the same teacher's VAM score for the other:
If the NYC value-added formula accurately measured teacher performance, you would expect there to be some correlation between a teacher's ability to teach, say, 7th grade math and that same teacher's ability to teach 8th grade math. That would show up on this graph as a cluster of data points on a diagonal line rising from bottom-left to top-right. Instead, the VAM scores are almost completely random.
Rubinstein found a minuscule correlation coefficient of only 0.24. The average difference between the two scores was nearly 30 points, and 10 percent of teachers had differences of more than 60 points. And he got similar near-random results when plotting the value-added scores of elementary school teachers teaching different subjects to the same students in the same classroom in the same year.
"I hope that these two experiments ... bring to life the realities of these horrible formulas," Rubinstein writes, adding that "the absurdity of these results should help everyone understand that we need to spread the word since calculations like these will soon be used in nearly every state."
Including, alas, Washington, thanks in large part to "reformers" who find it cheaper and/or easier to blame teachers (and their unions) for our schools' problems than to advocate for the tax revenue necessary to pay for reforms like universal pre-school and full-day kindergarten that actually work.